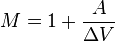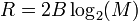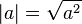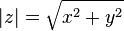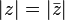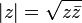Eclekticinema

Deseo y Motivación.

En su obra “Motivations and Personality”, publicada por Harper and Row en 1954, el psicólogo Abraham H. Maslow propuso una teoría de motivación basada en cinco categorías de necesidades humanas.

Necesidades: Falta o ausencia de cosas que son necesarias para la conservación de la vida. Crean impulsos que hacen que se busque una solución para mitigar o eliminar las carencias que las originan. Por ejemplo, la necesidad de respirar, beber o comer.

Deseos: Son impulsos más fuertes y específicas que las necesidades. Están orientados hacia la posesión o disfrute de algo concreto, que se conoce bien, que se antoja o que ya ha probado ser efectivo. Crean impulsos que pueden ser irresistibles hacia los objetos concretos. Ejemplo, el deseo de beber una determinada bebida o de comer una golosina concreta.

Motivaciones: Son fuerzas internas que impulsan al individuo a actuar en determinada forma. La motivación puede tener su origen en fuentes positivas o negativas. Por ejemplo, la codicia puede ser fuente de motivación para robar o el amor puede ser fuente de motivación para el desarrollo personal.

Impulsos: Son acciones que se llevan a cabo sin mayor reflexión, generalmente como resultado de actitudes o costumbres adquiridas. Por ejemplo, comprar impulsivamente una revista que está en la caja de un supermercado cuando un ama de casa se dispone a pagar el importe de sus compras.

Estímulos: Son situaciones, acciones o palabras que, originadas por alguien, incitan a obrar al sujeto receptor. Por ejemplo, un insulto incita a una reacción violenta o, por el contrario, una palabra amable incita a una respuesta similar.

Reacciones: Son la respuesta al estímulo recibido. Por ejemplo, el reconocimiento a un trabajo bien hecho puede tener como respuesta el mantenimiento o mejoramiento de la calidad lograda en el trabajo de persona afectada.


Maslow basa su teoría de motivaciones en las necesidades y los deseos de las personas. Sostiene que pueden aplicarse tanto en la vida familiar, como en el trabajo, la política o cualquier otra actividad humana. Define cinco niveles de necesidades y deseos, ordenados en forma ascendente, lo que indica que, en general, primero se debe satisfacer la primera categoría y después las siguientes. Sin embargo, reconoce también que un individuo puede estar involucrado en dos o tres niveles al mismo tiempo. Estas categorías son las siguientes:

FISIOLÓGICAS. Son las necesidades biológicas básicas de subsistencia, cuya satisfacción es urgente, impostergable más allá de un límite. Los motivadores son el hambre, la sed, el cansancio, el sueño, el apetito sexual. En el individuo, las reacciones frente a una carencia de este tipo pueden llegar a ser violentas.

DE SEGURIDAD. Son las necesidades psicológicas, que dan al individuo tranquilidad y confianza. Los motivadores son, entre otros, la certeza sobre algo, la tranquilidad que da una buena chapa en la puerta, el bienestar físico, la salud, el orden. Son los elementos que garantizan la conservación de lo que se ha logrado en el nivel anterior.

DE PERTENENCIA. Son las necesidades sociales. Están en el ámbito de las relaciones del individuo con los grupos en los que interactúa, sea en el ámbito familiar, social, religioso, de trabajo u otros. Los motivadores son el impulso hacia la interacción con otras personas semejantes a ellos, la aceptación en el grupo, el afecto, así como la necesidad o deseo de compartir actividades observando las normas y costumbres adoptadas por el grupo.

DE ESTIMACIÓN. Son las necesidades y deseos afectivos de carácter íntimo e individual, como el amor, la posesión del ser amado o de un objeto que satisfaga su ego. Es lo que se siente al adquirir un automóvil lujoso u otro bien que lo haga crecer en status ante su grupo. También está la necesidad o deseo de lograr el éxito, el prestigio y el reconocimiento por parte de los demás, el que otros conozcan una labor bien hecha, recibir un premio.

DE AUTO-REALIZACIÓN. Son los deseos de satisfacción personal que producen un sentimiento de triunfo, la sensación de poder y dominio, que incrementa el autoestima de la persona, lo que él o ella piensan sobre sí mismos. Es la culminación de las aspiraciones más deseadas, de alcanzar metas difíciles, de hacer algo que exija emplearse a fondo.

Eclekticinema

Según nuestra amada wikipedia Zeitgeist es originalmente una expresión del idioma alemán que significa "el espíritu (Geist) del tiempo (Zeit)". Denota el clima intelectual y cultural de una era.

40 Aniversario del Hombre en la Luna

La NASA, EEUU y el mundo entero celebrarán en 2009 el 40 aniversario de la llegada del hombre a la Luna y la ya mítica frase: "Un pequeño paso para el hombre, pero un gran salto para la humanidad", del comandante de la misión Apollo 11, Neil Armstrong, pronunciada el 20 de julio de 1969, cuando puso sus pies en la superficie lunar.

Un poco antes, el hombre comenzaba por primera vez a dejar el planeta y viajar hacia la luna. Entre 1968 y 1972 los astronautas del programa Apollo de la NASA probaron nuevas aeronaves y llegaron a destinos hasta entonces inexplorados.

Todo comenzó en mayo de 1961, cuando el presidente John F. Kennedy anunció su objetivo de mandar astronautas a la Luna antes de que finalizase la década de los 60. Tres semanas después, el astronauta del Mercury Alan Shepard se convirtió en el primer americano en el espacio.

Después de ocho años de trabajo en el que participaron miles de personas, el 20 de julio de 1969 el comandante Armstrong salió del módulo lunar y dio "un pequeño paso" en el enclave conocido como 'Mar de la Tranquilidad', definiendo este gesto como "un salto gigante para la humanidad". Armstrong viajó acompañado Edwin Aldrin Junior, piloto del módulo lunar; y Michael Collins, de 38 años y piloto del módulo de mando. El acontecimiento fue televisado en todo el mundo.

Durante el camino, no faltó la innovación y la improvisación, según reconoce la agencia norteamericana. En diciembre de 1968, antes que dejar que el módulo lunar retrasara el programa, la NASA cambió los planes para poder continuar. La misión Apollo 8 iría todo el camino hacia la luna y orbitaría sin el módulo lunar; fue el primer viaje tripulado del cohete Saturno V.

Seis de estas misiones -los Apollos 11, 12, 14, 15, 16 y 17- alunizaron y estudiaron mecánica sólida, meteoritos, seísmica, campos magnéticos y vientos solares, entre otras materias. Las misiones Apollo 7 y 9 probaron las naves orbitando la Tierra; la Apollo 10 orbitó la luna mientras se ensayaba el primer aterrizaje. Una explosión en el tanque de oxígeno forzó a la misión Apolo 13 a anular su alunizaje.

El nombre del programa se inspiró en los astronautas de la misión Apollo 1 Gus Grissom, Ed White y Roger Chaffee, que perdieron la vida en un incendio durante una prueba en la plataforma de lanzamiento en 1967.

Ley de Shannon - Hartley.

La ley debe su nombre a Claude Shannon y Ralph Hartley.
Hartley indicó que el número máximo de pulsos distintos que se pueden transmitir y recibir, de manera fiable, sobre un canal de comunicaciones está limitado por el rango dinámico de la amplitud de la señal y de la precisión con la cuál el receptor puede distinguir distintos niveles de amplitud.
De manera específica, si la amplitud de la señal transmitida se restringe al rango de [ − A... + A] voltios, y la precisión del receptor es +/- ΔV voltios, entonces el número máximos de pulsos distintos M está dado por:

Tomando la información para ser el logaritmo del número de los mensajes distintos que podrían ser enviados, Hartley después construyó una medida de la información proporcional al ancho de banda del canal y a la duración de su uso. A veces sólo se habla de dicha proporcionalidad cuando se cita a la ley de Hartley.
Posteriormente, Hartley combinó la observación de Nyquist, y su propia cuantificación de la calidad o ruido de un canal en términos del número de niveles de pulso que podían ser distinguidos, de manera fiable y denotados por M, para llegar a una medida cuantitativa de la tasa de información que se puede obtener.
La ley de Hartley se explica, cuantitativamente, de manera usual, como la tasa de información alcanzable de R(b / s): bits por segundo,

Hartley no resolvió, de manera precisa cómo el parámetro M debe depender de las estadísticas de ruido del canal, o cómo la comunicación podía ser fiable incluso cuando los pulsos individuales correspondientes a símbolos no se pudieran distinguir, de manera fiable, de los niveles de M; con las estadísticas del ruido gaussiano.
Los diseñadores de sistemas tienen que elegir un valor muy conservador de M para alcanzar la mínima tasa de error.
El concepto de una capacidad libre de errores aguardó hasta que Claude Shannon investigó sobre las observaciones de Hartley con respecto a la medida logarítmica de la información y las observaciones de Nyquist sobre el efecto de las limitaciones del ancho de banda del canal.
El resultado de la tasa de Hartley se puede ver como la capacidad de un canal M sin errores de 2B símbolos por segundo. Algunos autores se refieren a ello como capacidad. Pero ese supuesto canal, libre de errores, es un canal ideal, y el resultado es, necesariamente, menor que la capacidad de Shannon de un canal con ruido de ancho de banda B, que es el resultado Hartley-Shannon que se estimó más adelante.
Fue en los años 40, cuando Claude Shannon desarrolló el concepto de capacidad de un canal basándose, en parte, en las ideas que ya habían propuesto Nyquist y Hartley y formulando, después, una teoría completa sobre la información y la transmisión de esta, a través de canales.

C = W log ( 1 + S/N )

donde C es la capacidad del canal(taza de bits en bits/seg) o la rapidez de transmisión del mensaje y W es el ancho de banda del sistema en hertz. Con una C dada, podemos incrementar W y reducir S/N(relación señal a ruido) y viceversa.

Pistol en el Rio de la Plata

Esta entrada será dedicada a un lugar con mucho estilo;como es La Cantina "Rio de la Plata" en la ciudad de México,especificamente en Cuba 39 Esquina con Allende, Colonia Centro.
Lugar de memorables pedas entre amig@s y desconocid@s,un spot que no debe faltar .Gozen!





Este video no es en el river,pero ójala tubieran un soundtrack así de rifado,se imaginan??:

Eclekticinema

Bueno esta sección vendrá acompañada de mi cine favorité!Gozen

Valor Absoluto

Cualquier punto "a" tiene su representación en la recta real,el valor absoluto de un numero representa la distancia de éste al punto de origen.

El concepto de valor absoluto de un número real puede generalizarse a muchos otros objetos matemáticos, como son los cuerpos o espacios vectoriales.El valor absoluto está estrechamente relacionado con las nociones de magnutd y distancia en diferentes contextos matemáticos y físicos.

Desde un punto de vista geómetrico, el valor absoluto de un número real a corresponde a la distancia a lo largo de la recta numérica real desde a hasta el número cero. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. De hecho, el concepto de métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia.

Propiedades fundamentales

1. |a| ≥ 0
2. |a| = 0 ⇔ a = 0
3. |ab| = |a| |b|
4. |a+b| ≤ |a| + |b|

Otras propiedades

1. |-a| = |a|	Simetría
2. |a-b| = 0 ⇔ a = b	Identidad de Indiscernibles
3. |a-b| ≤ |a-c| + |c-b|	Desigualdad Triangular
4. |a-b| ≥ ||a| - |b||
5. |a/b| = |a| / |b| (si b ≠ 0)	Preservación de la dívision

Otras dos útiles inecuaciones son:

• |a| ≤ b ⇔ -b ≤ a ≤ b
• |a| ≥ b ⇔ a ≥ b b ≤ -a

por ejemplo:

Como los números complejos no conforman un conjunto ordenado en el sentido de los reales, la generalización del concepto no es directa, sino que requiere de la siguiente identidad, que proporciona una definición alternativa y equivalente para el valor absoluto:

De esta manera, dado cualquier número complejo de la forma

con x e y números reales, el valor absoluto o módulo de z está definido formalmente por:

Como los números complejos son una generalización de los números reales, es lógico que podamos representar a estos últimos también de esta forma:

De modo similar a la interpretación geométrica del valor absoluto para los números reales, se desprende del Teorema de Pitagoras que el valor absoluto de un número complejo corresponde a la distancia en el plano complejo de ese número hasta el origen, y más en general, que el valor absoluto de la diferencia de dos números complejos es igual a la distancia entre ellos.

Propiedades

El valor absoluto de los complejos comparte todas las propiedades vistas anteriormente para los números reales. Además, si

y

es el conjugado de z, luego podemos ver que:

Esta última fórmula, es la versión compleja de la primera identidad en los reales que mencionamos.

Funciones Pares e Impares

Una función f(x) es par si satisface la ecuación: f(-x)=f(x). Si una función es par entonces es simétrica con respecto al eje y.

Ej.La funcion coseno f(x)=cos (x)es par,ya que: cos(-x)=cos (x)

Una función f(x) es impar si satisface la ecuación: f(-x)=-f(x). Si una función es impar entonces es simétrica con respecto al origen

Esto significa geométricamente que dado un punto sobre la gráfica,existe otro punto en la gráfica equidistante con respecto al origen sobre una recta que pasa por el origen.

Ej.La funcion seno f(x)=sen (x)es impar,ya que: sen(-x)=-sen (x)