La ley debe su nombre a Claude Shannon y Ralph Hartley.
Hartley indicó que el número máximo de pulsos distintos que se pueden transmitir y recibir, de manera fiable, sobre un canal de comunicaciones está limitado por el rango dinámico de la amplitud de la señal y de la precisión con la cuál el receptor puede distinguir distintos niveles de amplitud.
De manera específica, si la amplitud de la señal transmitida se restringe al rango de [ − A... + A] voltios, y la precisión del receptor es +/- ΔV voltios, entonces el número máximos de pulsos distintos M está dado por:
Posteriormente, Hartley combinó la observación de Nyquist, y su propia cuantificación de la calidad o ruido de un canal en términos del número de niveles de pulso que podían ser distinguidos, de manera fiable y denotados por M, para llegar a una medida cuantitativa de la tasa de información que se puede obtener.
La ley de Hartley se explica, cuantitativamente, de manera usual, como la tasa de información alcanzable de R(b / s): bits por segundo,
Los diseñadores de sistemas tienen que elegir un valor muy conservador de M para alcanzar la mínima tasa de error.
El concepto de una capacidad libre de errores aguardó hasta que Claude Shannon investigó sobre las observaciones de Hartley con respecto a la medida logarítmica de la información y las observaciones de Nyquist sobre el efecto de las limitaciones del ancho de banda del canal.
El resultado de la tasa de Hartley se puede ver como la capacidad de un canal M sin errores de 2B símbolos por segundo. Algunos autores se refieren a ello como capacidad. Pero ese supuesto canal, libre de errores, es un canal ideal, y el resultado es, necesariamente, menor que la capacidad de Shannon de un canal con ruido de ancho de banda B, que es el resultado Hartley-Shannon que se estimó más adelante.
Fue en los años 40, cuando Claude Shannon desarrolló el concepto de capacidad de un canal basándose, en parte, en las ideas que ya habían propuesto Nyquist y Hartley y formulando, después, una teoría completa sobre la información y la transmisión de esta, a través de canales.
donde C es la capacidad del canal(taza de bits en bits/seg) o la rapidez de transmisión del mensaje y W es el ancho de banda del sistema en hertz. Con una C dada, podemos incrementar W y reducir S/N(relación señal a ruido) y viceversa.
Hartley indicó que el número máximo de pulsos distintos que se pueden transmitir y recibir, de manera fiable, sobre un canal de comunicaciones está limitado por el rango dinámico de la amplitud de la señal y de la precisión con la cuál el receptor puede distinguir distintos niveles de amplitud.
De manera específica, si la amplitud de la señal transmitida se restringe al rango de [ − A... + A] voltios, y la precisión del receptor es +/- ΔV voltios, entonces el número máximos de pulsos distintos M está dado por:
Posteriormente, Hartley combinó la observación de Nyquist, y su propia cuantificación de la calidad o ruido de un canal en términos del número de niveles de pulso que podían ser distinguidos, de manera fiable y denotados por M, para llegar a una medida cuantitativa de la tasa de información que se puede obtener.
La ley de Hartley se explica, cuantitativamente, de manera usual, como la tasa de información alcanzable de R(b / s): bits por segundo,
Los diseñadores de sistemas tienen que elegir un valor muy conservador de M para alcanzar la mínima tasa de error.
El concepto de una capacidad libre de errores aguardó hasta que Claude Shannon investigó sobre las observaciones de Hartley con respecto a la medida logarítmica de la información y las observaciones de Nyquist sobre el efecto de las limitaciones del ancho de banda del canal.
El resultado de la tasa de Hartley se puede ver como la capacidad de un canal M sin errores de 2B símbolos por segundo. Algunos autores se refieren a ello como capacidad. Pero ese supuesto canal, libre de errores, es un canal ideal, y el resultado es, necesariamente, menor que la capacidad de Shannon de un canal con ruido de ancho de banda B, que es el resultado Hartley-Shannon que se estimó más adelante.
Fue en los años 40, cuando Claude Shannon desarrolló el concepto de capacidad de un canal basándose, en parte, en las ideas que ya habían propuesto Nyquist y Hartley y formulando, después, una teoría completa sobre la información y la transmisión de esta, a través de canales.
C = W log ( 1 + S/N )
donde C es la capacidad del canal(taza de bits en bits/seg) o la rapidez de transmisión del mensaje y W es el ancho de banda del sistema en hertz. Con una C dada, podemos incrementar W y reducir S/N(relación señal a ruido) y viceversa.
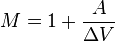
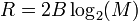






No hay comentarios:
Publicar un comentario